Don’t Be Intimidated By Sample Size, Learn About It!

Do estimate sample size. Don’t let sample size estimates be the enemy of test and learn culture. Learn why!

What is sample size and why does it matter?

When thinking about research studies, including online experiments, “sample size” refers to the number of participants included in the test. Sample size should be determined before running an experiment as it directly impacts test quality. It also impacts your ability as an optimizer to successfully read the results and take actions in light of those results moving forward. Sample size and calculating sample size is as important to planning an experiment as the challenge experience. Here are three risks you run if you don’t get the sample size right

1. If you choose a sample group that isn’t representative of the population, you risk rolling out a new experience that actually harms the KPI you sought to improve.

This is because the test results will not be generalizable over time. For example, say you run ecommerce for a retailer, and your boss is interested in testing during your big holiday sale because, “that’s when you get the most traffic so can do the most tests.” One of those tests is adding the promo code field to the cart, as today it only lives within checkout.  When you run the test, you see an increase in conversion rate—so much that even with increased promo code usage, the test is net positive for the business and you implement. But a few months later your boss comes back to you very concerned about first quarter sales.

Analysis shows that cart completion rate is lower than last year and for those who still convert, promo code usage is up. You conclude that though the new cart design worked really well during holiday when promo codes were plastered across the site, the results were not generalizable and the new experience actually created friction in the form of leaving the site to find a coupon.

2. If you choose a sample group that’s too small,  you run the risk of wasting resources on a test that will never give you a clear read on whether the challenger truly changed user behavior.

Setting statistical tests aside, let’s go back to the basics for this example.  When you flip a coin ten times and get six heads and four tails, do you assume that it is a rigged coin? What a hundred flips with 60 heads and 40 tails or a thousand flips with 600 heads and 400 tails? Even when we are rolling heads 50% more often than tails in each of these scenarios, it takes me (and probably you, too) at least 1,000 trials before I question the coin’s fairness. Before that point, I can still chalk this degree of variance up to chance.

An example of how choosing a group that’s too small often plays out with our ecommerce clients is the desire to test on a single product page instead of many product pages. We advise against this because sampling so little of the total population results in more inconclusive results. While you might save time during QA by testing on a single page, you are taking a tiny percentage of your “product page population” and then splitting tiny in half to run the A/B test. What you are left with is a super tiny sample size that will need to produce massive behavior change to reach significance. Plus, there is no guarantee that the insights gained from one product will scale with other products (see risk 1 in this list)!

3. If you choose a sample group that’s too large, you run the risk of wasting resources on behavior changes so miniscule that the business impact won’t be noticed and the cost to implement is too high to justify.

This problem comes up less often than the first two but still does get brought up when talking about hold-out groups or sites with more traffic than to know what to do with. If the latter sounds like you, our data scientists would love to talk to you!

If you’ve reached statistical significance and total sample size, and you’ve thoughtfully defined your statistical standards, you did it! Move on.

But what happens if you didn’t reach the lift you set out to find? First, it’s important to say that our POV is that your lift standard should be set at the smallest lift you’d have to see to build the business case to actually implement the change. Think about lift as “needed lift” instead of “estimated lift.”  If you don’t hit needed lift and reach your estimated sample size, continuing to run is not only a bad use of resources, it’s the experimentation world’s form of cheating, called p-hacking.  There are whole articles written on p-hacking, so we won’t go too deep into it here, but if you’re interested in learning about it – here are some great articles to check out.

• Scientific method: Statistical errors
• Science, Trust And Psychology In Crisis
• We're All 'P-Hacking' Now

What impacts sample size requirements?

Sample size requirements are impacted by several factors.

• Type I error (false positive) control: Every experiment has a risk of a “False Positive” (Type 1) error. Think of an erroneously positive medical test result found to be incorrect with further testing.  Reducing your risk of this type of error requires setting a higher “Confidence Level”. The higher you set your Confidence Level, the lower your risk for a False Positive and the more samples you will need to reduce that risk. Important note – the risk of a False Positive is not actually that a “win” becomes a “loss” – but only that a “win” is actually flat. Also, “positive” here really means “different from control” – whether positive or negative.
• Type II error (false negative) control: Every experiment also has a risk of a “False Negative (Type II) error. These are the erroneously negative test results that miss a true positive. Using the medical test example, this type of error would mistakenly state that nothing was going on when it actually was. Reducing your risk of this type of error requires setting higher “Power.” Think of power like the microscopes you used in your lab classes in school. When looking at increasingly smaller objects, you increased the power on your microscope to see better. It’s the same here. Increasing power allows you to see smaller differences but requires more samples. Greater sample size = greater power.
• Baseline KPI Rate: The primary metric or “KPI” (Key Performance Indicator) for your experiment also impacts the required sample size. Selecting a metric that is far away from the activity being tested will naturally introduce noise into your analysis requiring more power to see through the noise for the signal. Similarly, selecting a primary metric that is large will require less power (smaller sample) to see a change – whether that change is small or large. Using the analogy of the microscope, this concept is easy to understand: If we start with a larger object, we need less “power” (fewer samples) to “see” (measure).
• MDE (Minimal Detectable Effect):  It should be clear by now that the size of what you are attempting to detect with your “microscope” impacts the amount of samples required to see it (power). When you make a minor change to an experience, you can also expect a small impact to behavior, which would require a much larger sample to validate. If you make a very large change, you will not need as many samples to get a statistically significant read on the results. (If you remove the add to cart button from a page, it will not take you long to figure out that this removal has a negative impact on your conversion rate. But changing “Add to Cart” to “Add to Basket” will require more data to decide if “B” is better than “A”).

How do I calculate sample size?

Fortunately, you don’t have to calculate your sample size by hand! There are plenty of free, online calculators available to help you. Each calculator listed below has different required inputs as well as different reasons for using each.

• Standard Sample Size Calculator: Use this calculator if you already know what the minimum needed lift is to implement the change and want to know how long a test will need to run. Screenshots below.

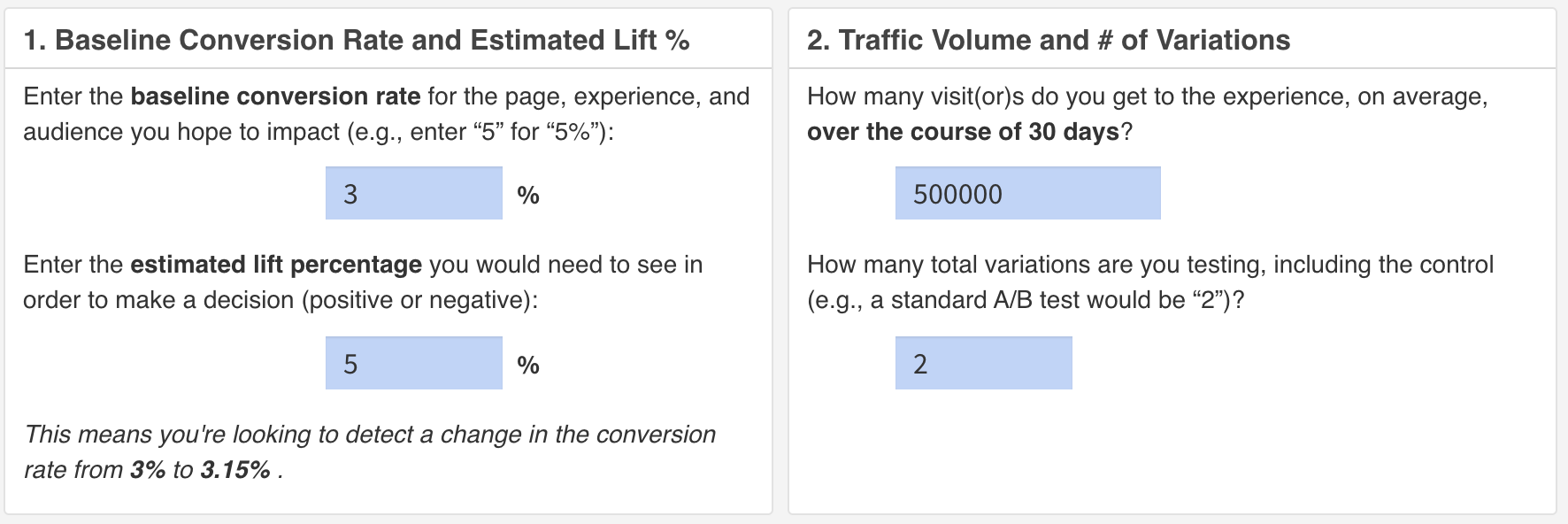
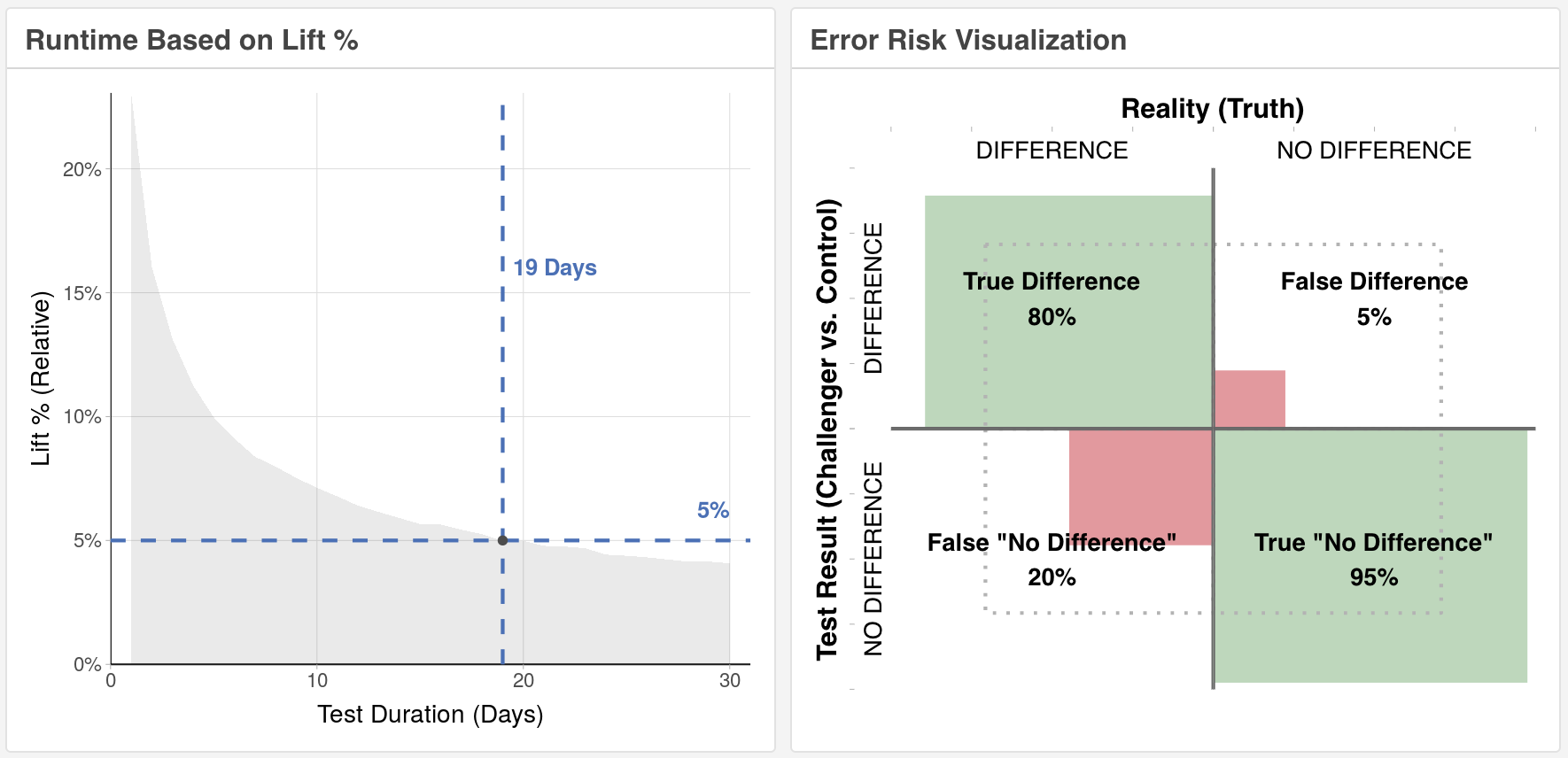
• Runtime Sample Size Calculator – Use this calculator when you’re not sure what the minimum lift should be and/or you have a clear understanding of how long you’re willing to let the test run.
• Sequential Test Design Calculator – Use this calculator when the standard calculator gives you a runtime longer than you like or when you want to be able to “peek” and end a test if you surpass a decision boundary early.

FAQs

Do I still have to estimate sample size if I’m running experiment (Bayes, Sequential, etc.)?

The short answer is… sorta. There are no absolutes, but having an understanding of the sample size – even when it’s only the potential sample size for a Bayesian or Sequential test design helps you both with planning and prioritization. For example, if your sample size estimation tells you that experiment A could require 3 months to get an answer, but experiments B-Z could all be run in that same time frame, you might choose to de-prioritize experiment A or find a way to redesign it to shorten the runtime.

What if my available population is smaller than my minimum sample size?

1. Consider whether any of the levers listed above could be adjusted. For example, is the risk of a false positive not that bad? Are you just trying to pick the “best” headline?
2. Is the cost of rolling out a false positive (i.e., true flat) minimal? Maybe you can decrease your Confidence Level.
3. Is there a different metric that could help you get your answer? For example, instead of looking at the bottom of the funnel for orders/visitors, could you look instead at video views, clicks on your offer, or add to cart
4. Lastly, is there any way to increase how dramatic your experiment is so that you have a larger expected impact? And don’t forget, you can always use a Sequential Test Design even with a test platform that does not use sequential methods using a Sequential Design Calculator.
5. Also, check out Dr. Elea Feit’s TLC conversation about profit-maximizing A/B testing for small sample sizes.

Is it possible to have too many samples?

Yes! If your sample size is too large, you run the risk of finding statistically significant results that have no practical implications to your business. I’ve often felt that the oft-shared “three types of lies” quote exists because of this simple truth: With a large enough sample size, you can find / prove anything to be “true” with data.

There is even data to suggest a correlation exists between the number of babies born and the number of storks. Clearly, these two data points are neither connected nor meaningful, but they move in tandem. The point is, with a large enough sample size, you may find correlations that have little to no business impact.

‍

Final Thoughts

Ultimately, the pushback against sample size estimation is most often that companies want increasingly faster testing velocity that their traffic can’t statistically handle. That’s where we fit in. Further has a team of optimization professionals with decades of experience not letting sample size estimations be the enemy of test and learn culture. Reach out below for more information.

Want help planning your next experiment? We can help!